Ch2 Components of Matter
Element – simplest type of matter with unique physical and chemical properties (only one kind of atom)
Molecule – independent structural unit consisting of two or more atoms that are chemically bound together
Compound – composed of two or more different elements that are chemically bound together
Mixture – a group of two or more substances (elements and/or compounds) that are physically intermingled.
Laws
Mass Conservation – the total mass of substances does not change during a chemical reaction.
Definite Composition – a particular chemical compound is composed of the same elements in the same
parts (fractions) by mass.
Multiple Proportions – if elements A and B react and form two different compounds, the different masses of B
that combine with a fixed mass A can be
expressed by a ratio of small whole numbers.
Read postulates 1-4, page 46
Mass Conservation – Atoms cannot be created or destroyed, cannot be converted into other types of atoms, a
chemical reaction where the only difference is the combination of atoms cannot produce a
mass change.
Definite Composition – A compound has a specific ratio of atoms, so each elements has a fixed fraction of mass
Multiple Proportions – Atoms of same element have same mass, so if different masses of element B combine
with a fixed amount of A, then the resulting compound will differ by a small whole
number ratio.
Nuclear Atom Model
Cathode Ray Tube experiment – J.J. Thoompson
Millikan Oil Drop experiment
Atomic Theory Today
Atom – “electrically neutral, spherical entity composed of a positively charged central nucleus surrounded by one or more negatively charged electrons.”
Nucleus – consists of protons and neutrons (except for hydrogen).
Atomic Number (Z) – number of protons, “each element has a different atomic number from that of any element”
Mass Number (A) – total number of neutrons and protons in atom (number of neutrons = A – Z)
Atomic Symbol (X) – symbol of element (examples C- carbon, O – oxygen, Na – sodium, etc…)
Isotopes – A particular element have different mass numbers due to the number of neutrons it contains in the nucleus. Sample Problem 2.2 (pg 53)
Read “A Modern Assessment of the Atomic Theory” pgs 55 – 56
Periodic Table
Figure 2.11
Increasing Atomic Number as you go from left to right and top to bottom.
Period – rows of periodic table
Groups – columns of period table
Main group elements – The eight A groups
Transition Elements – The ten B groups
Types of elements – Metals, Non-metals, Metalloids
Bonding
Ionic compounds – transfer of electrons from one element to another. Typical when non-metal and metal react.
Cation – positively charged ion
Anion – negatively charged ion
Neutral – no net charge
Noble gas relationship – metals tend to lose electrons and non-metals tend to gain electrons to “form
ions with the same number of electrons as in the nearest noble gas.” Fig. 2.14, 2.15
Covalent compounds – sharing electrons between elements, usually occurs when a non-metal reacts with a non-metal. “Most covalent substances consist of molecules, whereas no molecules exist in a sample of an ionic compound.”
Chemical Formulas
Empirical Formula – relative number of elements in compound
Molecular Formula – actual number of elements in compound
Structural Formula- shows number of atoms and the types of bonds between them.
Naming
read pgs 64 – 71
Molecular Mass
Sum of Atomic masses of all elements in molecule (or
compound). Sample Problem 2.13 (pg 72)
Ch3
Mole – SI unit for amount of substance. Number of entities related to mole by Avogadro’s number
(NA = 6.022 x 1023 entities)
Molar Mass – mass per mole (g/mole)
Look at pg 90 and sample problem 3.1 to convert between mass, moles, and entities
Mass percent of element = ![]()
Look at Sample Problem 3.4,3.5, and 3.6 to obtain empirical
formulas and molecular formulas of unknown compounds.
Balancing Chemical Equations – the same number of each type of atom must appear on both sides of the chemical equation (products and reactants).
Calculating Amounts of Reactants and Products pg 106 gives a good explanation
Limiting Reagent
– “the reactant that yields the lower amount of product.”
Percent yields =
![]()
Problem 69 –
Solid Iodine trichloride (ICl3) is prepared by reaction between solid Iodine (I2(s) ) and gaseous chlorine (Cl2(g)) to form monochloride crystals (ICl(s)), followed by treatment with additional chlorine (Cl2(g)).
a) Write a balance equation for each step.
b) Write an overall balance equation for the formation of iodine trichloride.
c) How many grams of Iodine are needed to prepare 31.4 kg of final product?
Step 1) I2(s) + Cl2(g) à 2ICl(s)
Step 2) ICl(s) + Cl2(g) à ICl3(s)
b) We want to show only initial Reactants going to final Products:
I2(s) + Cl2(g) à ICl3(s)
Need to somehow balance and cancel out the intermediate products. Add step 1) and step 2). Remember to subtract the compounds that appear on different sides of the equations. By multiplying Step 2) by 2 (to cancel out ICl3) we get:
I2(s) + Cl2(g) à 2ICl(s)
2[ICl(s) + Cl2(g) à ICl3(s)]
----------------------------------
I2(s) + 3Cl2(g) à 2ICl3(s)
Check that the chemical equation is balanced:
Reactants Products
I 2 2
Cl 6 6
Molecular Mass of ICl3 :
I – 126.9
Cl – 3x 35.45
-----------------
233.25 g/mol ICl3
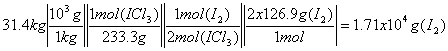
Stoichiometry
Solute – smallest amount in the solution
Solvent – largest amount in the solution
Molarity (concentration) M– in units of moles of solute per Liter of solution
Dilution
M1V1 = M2V2 ,
where M1 is the higher concentration (starting value) and M2
is the diluted solution, V1 and V2 are their respective
volumes.
Ch 6 Thermochemistry
Energy
Law of Energy Conservation – “the total energy of the universe is constant.”
DEuniverse
= DEsystem + DEsurrounding = 0
System – part of universe we are going to observe
Surroundings – everything else relevant to the change (except for system).
Change in energy: final – initial = Product – Reactants
Heat – thermal energy, q.
Work – “all other forms of energy transfer” (mechanical, electrical, etc…), w.
![]()
Heat
Flowing out of system, -q => -DE
Flowing into a system , +q => +DE
Units
Joule (J) = kg m2 s-2, 4.184 J = 1 cal
State Functions
Property only dependent on the current state of the system, not on the path system took to reach state.
Enthalpy
Internal Energy plus product of Pressure (P) and Volume (V)
Change in Enthalpy equals the heat gained or lost (by the system) at constant pressure
Endothermic – absorbs heat, increase in enthalpy of the system
Exothermic – release of heat, decrease of enthalpy of the system
Types
Heat of Combustion – Enthalpy change in Combustion reaction
Heat of formation – Enthalpy change to form a compound from its elements
Heat of fusion – Enthalpy change of the physical process of melting
Heat of vaporization – Enthalpy change of the physical process of vaporization (boiling)
Calorimetry
Specific heat Capacity (c) – Energy required to raise
Temperature by 1oC of 1g of pure substance (J/goC)
Heat capacity – Energy required to raise Temperature by 1oC of entire substance (J/oC)
q= m c DT (m –mass, c – specific heat capacity, DT – change in Temperature)
Sample Problems 6.4, 6.5 (pgs 234-236)
Hess’s Law of Heat of Summation
The overall process has a final Enthalpy change that can be summed up by the individual Enthalpy changes for each step.
![]() (sample problem 6.9,
chapter problems6.81,86,95)
(sample problem 6.9,
chapter problems6.81,86,95)
Ch 7
Matter and Energy
Matter and Energy are related, and both have properties of waves and particles (wave-particle duality).
Property Examples: Light (Energy, classically thought of as a wave) – wave nature (diffraction pattern), also particle nature (light is made up of photons)
Electron (classically thought of as matter) – wave nature (has wave-like orbitals), also particle nature (localized electron density)
Equations relating matter to energy:
![]()
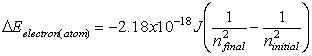
![]()
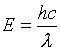
E – energy, m – mass, c –
speed of light, n – energy level, h – planck’s constant, ![]() - frequency, l -
wavelength
- frequency, l -
wavelength
Electromagnetic Spectrum
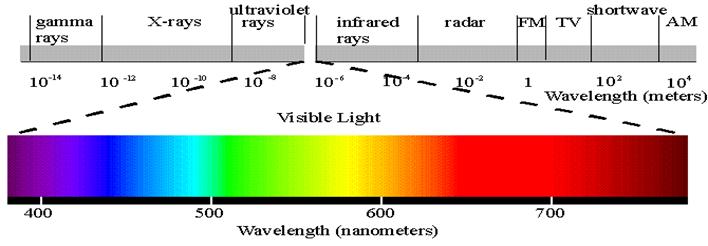
Wave Nature of Light
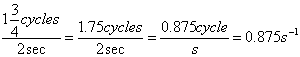
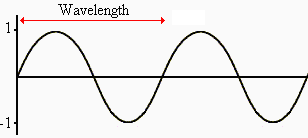
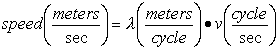
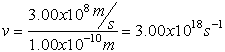
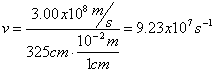
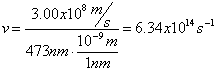
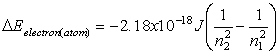
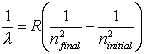
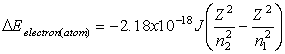 ,
,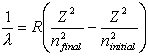
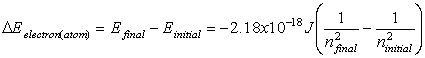
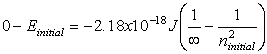
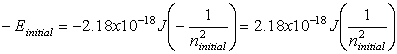
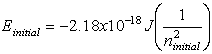
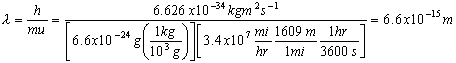
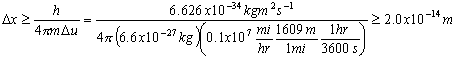
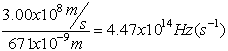
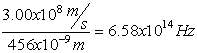
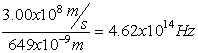
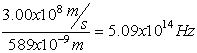
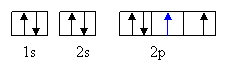 Z= 8
Oxygen. For sixth e—n =
2, l = 1 ml = 0 ms = +1/2
Z= 8
Oxygen. For sixth e—n =
2, l = 1 ml = 0 ms = +1/2